Practical No. 1: Set Theory
a. Inclusion Exclusion principle.
Aim: Write a code in Scilab to Find number of mathematics students taking at least one of the three languages French (F) German (G) or Russian (R) considering the following data. Use Inclusion Exclusion principle.
Language
No. of Students Studying
French
65
German
45
Russian
42
French and German
20
German and Russian
15
Russian and French
25
French and German and Russian
08
Scilab Code:
clc;clear;
F=65;
G=45;
R=42;
FnG=20;
GnR=15;
RnF=25;
FnGnR=8;
//by inclusion exclusion principle
ForGorR=F+G+R-FnG-GnR-RnF+FnGnR;
disp("Number of Mathematics students studying atleast one of the 3 languages",ForGorR);
Output:
"Number of Mathematics students studying atleast one of the 3 languages"
100.
b. Power Set
Aim: Given a set A=[1,2,3,4,5] where 1 represent the onion , 2 represent the tomato , 3 is carrot , 4 is cabbage and 5 is cucumber. Write a Sci-lab code to find
a. Total number of eatables available.
b. Numbers of different salads that can be prepared using the given eatables.
Scilab Code:
clc;clear;
A=[1,2,3,4,5];
p=length(A);
disp(p,"Total number of eatables available are:");
n=2^p-1;
disp(n,"number of different salads that can be prepared using the given eatables:");
Output:
"Total number of eatables available are:"
5.
"number of different salads that can be prepared using the given eatables:"
31.
c. Mathematical Induction
AIM: Write a program in Scilab for the following:
If $𝑈_𝑛 = 3𝑈_{𝑛−1} − 2𝑈_{𝑛−2}, 𝑈_1 = 3, 𝑈_2 = 5$ then prove that $𝑈_𝑛=1+2^𝑛, ∀𝑛 ∈ ℕ$.
Scilab Code:
clc;clear;
U=[];
P=[];
U(1)=3;
U(2)=5;
k=0;
for i=1:10
P(i)=1+2^i
if i>=3 then
U(i)=3*U(i-1)-2*U(i-2);
end
if P(i)==U(i) then
k=k+1;
end
end
if k==10 then
disp('Hence Un=1+2^n for all n belongs to set of natural numbers.');
else
disp('Statement is not true.');
end
Output:
"Hence Un=1+2^n for all n belongs to set of natural numbers."
Practical No. 2: Functions and Algorithms
a. Recursively defined functions
Aim: Write a scilab code for defining and using a recursive function for calculating the factorial of a number.
OR
Write a scilab code to find the factorial of 4 by recursive function.
Scilab Code:
clc;clear;
function [k]=fact(a)
if(a<0|a>200)
disp("Invalid");
break;
else
if(a==1|a==0)
k=1;
else
k=a*fact(a-1);
end
end
endfunction
disp("the value of 4! is",fact(4))
Output:
"The value of 4! is"
24.
b. Cardinality
Aim: Find cardinality of set A={x,y,z} and B={1,3,5,7,9}
Scilab Code:
clc;clear;
x=1;
y=2;
z=3;
A=[x,y,z];
B=[1,3,5,7,9];
n=length(A);
m=length(B);
disp("cardinality of set A is :",n);
disp("cardinality of set B is:",m);
Output:
"cardinality of set A is :"
3.
"cardinality of set B is:"
5.
c. Polynomial evaluation
Aim: Write a code in scilab to evaluate the following polynomials for the value 5 OR By the horner’s method find out the value of polynomial at x=5.
a. $2𝑥^3 − 7𝑥^2 + 4𝑥 − 15$
b. $3𝑥^3 + 𝑥^2 − 8𝑥 + 3$
Scilab Code:
clc;clear;
x=poly(0,"x");
p1=2*(x^3)-7*(x^2)+4*x-15;
disp("The first polynomial is",p1)
k1=horner(p1,5);
disp("Value of the polynomial at x=5 is",k1)
p2=3*(x^3)+x^2-8*x+3;
disp("The second polynomial is",p2)
k2=horner(p2,5);
disp("Value of the polynomial at x=5 is",k2)
Output:
"The first polynomial is"
-15 +4x -7x^2 +2x^3
"Value of the polynomial at x=5 is"
80.
"The second polynomial is"
3 -8x +x^2 +3x^3
"Value of the polynomial at x=5 is"
363.
d. Greatest Common Divisor
Aim: Find out the GCD of 258, 60 and 355, 6.
Or Write a scilab code to demonstrate the use of the gcd() function.
Scilab Code:
clc;clear;
V=int([258,60]);
disp("The gcd of the two numbers 258 and 60 is",gcd(V));
W=int([355,6]);
disp("The gcd of the two numbers 355 and 6 is",gcd(W));
Output:
"The gcd of the two numbers 258 and 60 is"
6.
"The gcd of the two numbers 355 and 6 is"
1.
Practical No. 3: Probability Theory 1
a. Sample space and events
Aim: Write SCILAB programs to demonstrate sample space and events.
A fair dice is tossed. Find the sample space.
a. The event that an even or a prime number occurs.
b. The event that an odd prime number.
c. The event that a prime number does not occur.
Scilab Code:
clc;clear;
S=[1,2,3,4,5,6];
A=[2,4,6];
B=[1,3,5];
C=[2,3,5];
disp("The sample space for the given random experiment is:",S);
disp("sample space for the event that an even or a prime number occurs",union(A,C));
disp("sample space for the event that an odd prime number occurs",intersect(B,C));
disp("sample space for the event that a prime number does not occur",setdiff(S,C));
Output:
"The sample space for the given random experiment is:"
1. 2. 3. 4. 5. 6.
"sample space for the event that an even or a prime number occurs"
2. 3. 4. 5. 6.
"sample space for the event that an odd prime number occurs"
3. 5.
"sample space for the event that a prime number does not occur"
1. 4. 6.
b. Finite probability spaces
Aim: Write a code in scilab to calculate the probability. Let a card be selected from an ordinary deck of 52 playing cards. Find
a. Probability of selecting spade card.
b. Probability of selecting a face card.
c. Probability of selecting a spade face card.
OR
Write a code in scilab to calculate the probability of selecting a spade face card from a deck of 52 cards.
Scilab Code:
clc;clear;
disp("Experiment: a card is selected from a deck of 52 cards");
disp("A is the event of the selected card being a spade");
disp("B is the event of the selected card being a face card");
disp("AB is the event of the selected card being a spade face card");
T=52;
A=13;
PA=A/T;
B=12;
PB=B/T;
AB=3;
PAB=AB/T;
disp("probability of selecting a spade",PA);
disp("probability of selecting a face card",PB);
disp("probability of selecting a spade face card is",PAB);
Output:
"Experiment: a card is selected from a deck of 52 cards"
"A is the event of the selected card being a spade"
"B is the event of the selected card being a face card"
"AB is the event of the selected card being a spade face card"
"probability of selecting a spade"
0.25
"probability of selecting a face card"
0.2307692
"probability of selecting a spade face card is"
0.0576923
c. Equiprobable spaces
Aim: Suppose an uniform die is rolled and let A be an event that an even number appears, B be an event that an odd number appears and C be an event that a prime number appears. Write a code in scilab to calculate the probability of the events $A, B, C, A\cup C, A\cup B, B\cap C, C^c$
Scilab Code:
clc;clear;
S=[1,2,3,4,5,6];//sample space for the rolling of a dice
A=[2,4,6];//event that an even number occurs
B=[1,3,5];//event that an odd number occurs
C=[2,3,5];//event that a prime number occurs
AorC=union(A,C);//event that an even or a prime number occurs
AorB=union(A,B);//even that an even or an odd number occurs
BandC=intersect(B,C);//event that an odd prime number occurs
complimentC=setdiff(S,C);//event that a prime number does not occur
PA=length(A)/length(S);
disp('Probability of occurrence of event A:',PA);
PB=length(B)/length(S);
disp('Probability of occurrence of event B:',PB);
PC=length(C)/length(S);
disp('Probability of occurrence of event C:',PC);
PAorC=length(AorC)/length(S);
disp('Probability of the event that an even or a prime number occurs:',PAorC);
PAorB=length(AorB)/length(S);
disp('Probability of the event that an even or an odd number occurs:',PAorB);
PBandC=length(BandC)/length(S);
disp('Probability of the event that a prime odd number occurs:',PBandC);
PcomplimentC=length(complimentC)/length(S);
disp('Probability of the event that prime number does not occur:',PcomplimentC);
Output:
"Probability of occurrence of event A:"
0.5
"Probability of occurrence of event B:"
0.5
"Probability of occurrence of event C:"
0.5
"Probability of the event that an even or a prime number occurs:"
0.8333333
"Probability of the event that an even or an odd number occurs:"
1.
"Probability of the event that a prime odd number occurs:"
0.3333333
"Probability of the event that prime number does not occur:"
0.5
d. Addition Principle
Aim: Suppose a student is selected at random from 100 students where 30 are taking mathematics, 20 are taking chemistry and 10 are taking mathematics and chemistry. Write a code in scilab to calculate the probability p that the student is taking mathematics or chemistry.
Scilab Code:
clc;clear;
disp("Experiment: selection of a student out of 100 students");
M=30;
C=20;
T=100;
PM=M/T;
PC=C/T;
MnC=10;
PMnC=MnC/T;
PMorC=PM+PC-PMnC;
disp("probability of the selected student taking Mathematics or Chemistry",PMorC);
Output:
"Experiment: selection of a student out of 100 students"
"probability of the selected student taking Mathematics or Chemistry"
0.4
Practical No. 4: Probability Theory 2
a. Conditional Probability
Aim: A bag contains 12 items of which four are defective. Three items are drawn at random, one after the other. Write a code in scilab to find
a. The probability that the first item drawn is non-defective.
b. The probability that the three item drawn is non-defective.
Scilab Code:
clc;clear;
disp("A bag contains 12 items of which four are defective. Three items are drawn at random, one after the other");
s=12;
d=4;
Pf=(s-d)/s;
disp("probability that the first item drawn is non-defective",Pf);
Pe=Pf*[(s-d-1)/(s-1)]*[(s-d-2)/(s-2)];
disp("probability that all three items are non-defective",Pe);
Output:
"A bag contains 12 items of which four are defective. Three items are drawn at random, one after the other"
"probability that the first item drawn is non-defective"
0.6666667
"probability that all three items are non-defective"
0.2545455
b. Multiplication theorem for conditional probability
Aim: A class has 14 boys and 6 girls. Suppose 4 students are selected at random from the class. Write a programme in Scilab to find the probability that they are all boys.
Scilab Code:
clc;clear;
t=20;//total no. of students in class
b=14;//no. of boys in class
P1=b/t;//probability that first selected student is a boy
P2=(b-1)/(t-1);//probability that second selected student is a boy
P3=(b-2)/(t-2);//probability that third selected student is a boy
P4=(b-3)/(t-3);//probability that forth selected student is a boy
P=P1*P2*P3*P4;
disp('Probability that all four selected students are boy:',P);
Output:
"Probability that all four selected students are boy:"
0.2066047
c. Independent events
Aim: Consider a family with three children and let A be an event that first child is a boy, B be an event that second child is a boy and C be an event that two successive children are boy. Write a programme in Scilab to find which of the two events are independent events.
Scilab Code:
clc;clear;
B=1;//boy child
G=2;//girl child
S=[111,112,121,122,211,212,221,222];//sample space
A=[111,112,121,122];//event that first child is boy
B=[111,112,211,212];//event that second child is boy
C=[111,112,211];//event that two successive children are boy
PA=length(A)/length(S);
disp('Probability of A is:',PA);
PB=length(B)/length(S);
disp('Probability of B is:',PB);
PC=length(C)/length(S);
disp('Probability of C is:',PC);
AandB=intersect(A,B);
AandC=intersect(A,C);
BandC=intersect(B,C);
PAandB=length(AandB)/length(S);
disp('Probability of the event AnB is:',PAandB);
PAandC=length(AandC)/length(S);
disp('Probability of the event AnC is:',PAandC);
PBandC=length(BandC)/length(S);
disp('Probability of the event BnC is:',PBandC);
if((PA*PB)==PAandB)
disp('A and B are independent.');
else
disp('A and B are dependent.');
end
if((PA*PC)==PAandC)
disp('A and C are independent.');
else
disp('A and C are dependent.');
end
if((PB*PC)==PBandC)
disp('B and C are independent.');
else
disp('B and C are dependent.');
end
Output:
"Probability of A is:"
0.5
"Probability of B is:"
0.5
"Probability of C is:"
0.375
"Probability of the event AnB is:"
0.25
"Probability of the event AnC is:"
0.25
"Probability of the event BnC is:"
0.375
"A and B are independent."
"A and C are dependent."
"B and C are dependent."
d. Repeated trials with two outcomes
Aim: Whenever three players viz. A, B and C, play together, their respective probability of winning are 0.5, 0.3 and 0.2. They played two matches. Write a programme in Scilab to
(i) Describe the probability space S.
(ii) Find the probability that the same player wins both the matches.
Scilab Code:
clc;clear;
P1=0.5;//probability that player A wins the match
P2=0.3;//probability that player B wins the match
P3=0.2;//probability that player C wins the match
S2=[11,12,13,21,22,23,31,32,33];//sample space S2 where 11 means player A wins both mathches and 12 means player A wins first match and player B wins second match etc
P11=P1*P1;//probability that player A wins both the matches
disp('Probability that player A wins both the matches:',P11);
P22=P2*P2;//probability that player B wins both the matches
disp('Probability that player B wins both the matches:',P22);
P33=P3*P3;//probability that player C wins both the matches
disp('Probability that player C wins both the matches:',P33);
disp('Probability that same player wins both matches:',P11+P22+P33);
Output:
"Probability that player A wins both the matches:"
0.25
"Probability that player B wins both the matches:"
0.09
"Probability that player C wins both the matches:"
0.0400000
"Probability that same player wins both matches:"
0.38
Practical No. 5: Counting 1
a. Sum rule principle
Aim: Suppose there are 8 male professors and 5 female professors teaching a calculus class. Write a programme in Scilab to find in how many ways a student can choose professor?
Scilab Code:
clc;clear;
M=8;
F=5;
T=M+F;
disp("number of ways a student can choose a calculus professor",T);
Output:
"number of ways a student can choose a calculus professor"
13.
b. Product rule principle
Aim: A license plate contains two letters followed by three digits where first digit cannot be zero. Write a scilab code to find total numbers of plates can be printed.
Scilab Code:
clc;clear;
a=26;
m=a*a;
p=10;
n=(p-1)*p*p;
k=m*n;
disp("Total number of license plates that can be printed is",k);
Output:
"Total number of license plates that can be printed is"
608400.
c. Factorial
Aim: Write a scilab code to find out the factorial of (i) 6 (ii) 8 .
Scilab Code:
clc;clear;
a=factorial(6);
disp("The factorial of 6 is:",a);
b=factorial(8);
disp("The factorial of 8 is:",b);
Output:
"The factorial of 6 is:"
720.
"The factorial of 8 is:"
40320.
d. Binomial coefficients
Aim: Write a scilab code to simplify the binomial coefficient (i) $^{10}C_7$ (ii) $^{10}C_3$
Scilab Code:
clc;clear;
function [k]=binomial(n, r)
k=factorial(n)/(factorial(r)*factorial(n-r));
endfunction;
disp("value of 10C7 is",binomial(10,7));
disp("value of 10C3 is",binomial(10,3));
Output:
"value of 10C7 is"
120.
"value of 10C3 is"
120.
Practical No. 6: Counting 2
a. Permutations
Aim: A teacher is preparing an examination time table for 5 papers to be held on 5 consecutive days. Write a scilab code to find how many different time table can she make?
Scilab Code:
clc;clear;
function [k]=prmtn(n,r)
k=factorial(n)/factorial(n-r);
endfunction
n=5;//number of days available
r=5;//number of papers to schedule
ans1=prmtn(n,r);
disp('Number of different time tables:',ans1);
Output:
"Number of different time tables:"
120.
b. Permutations with repetitions
Aim: Write a scilab code to find number of words can be formed by using letters of the word
(i) UNUSUAL
(ii) SOCIOLOGICAL
Scilab Code:
clc;clear;
function [k]=rpermu(n, r1, r2, r3, r4)
k=factorial(n)/(factorial(r1)*factorial(r2)*factorial(r3)*factorial(r4));
endfunction
//number of words can be formed by using letters of the word UNUSUAL
a=7;//total number of letters in the word UNUSUAL
b=3;//letter U is repeated 3 times
p=rpermu(a,b,0,0,0);
disp('Number of words can be formed by using letters of the word UNUSUAL is:',p);
Output:
"Number of words can be formed by using letters of the word UNUSUAL is:"
840
c. Combinations
Aim: Write a scilab code to find in how many ways can a committee of 8 people be formed out of a group of 10 men and 5 women?
Scilab Code:
clc;clear;
function [k]=comb(n, r)
k=factorial(n)/(factorial(r)*factorial(n-r));
endfunction
m=10;//total number of men
w=5;//total number of women
r=8;//number of people to select
c=comb(m+w,r);
disp('Number of ways to form a committee of 8 out of a group of 10 men and 5 women is:',c);
Output:
"Number of ways to form a committee of 8 out of a group of 10 men and 5 women is:"
6435.
d. Combinations with repetitions
Aim: A bangel shop sells 5 kinds of bagels. Write a scilab code to find the number of ways a customer can buy: (a) 8 bangels; (b) a dozen bangels.
Scilab Code:
clc;clear;
function [k]=rcomb(r, m)
k=factorial(r+(m-1))/(factorial(r)*factorial(m-1));
endfunction
r1=8;//number of objects to select
m=5;//kinds of objects available
c1=rcomb(r1,m);
disp('Number of ways a customer can buy 8 bangles from 5 different kinds of bangles is:',c1);
r2=12;//number of objects to select
c2=rcomb(r2,m);
disp('Number of ways a customer can buy 12 bangles from 5 different kinds of bangles is:',c2);
Output:
"Number of ways a customer can buy 8 bangles from 5 different kinds of bangles is:"
495.
"Number of ways a customer can buy 12 bangles from 5 different kinds of bangles is:"
1820.
Practical No. 7: Counting 3
a. Ordered partitions
Aim: Let the set S has 7 elements. Write a scilab code to find the number of ordered partitions of S into 3 cells with 2, 2 and 3 elements.
Scilab Code:
clc;clear;
n=7;//total number of elements in S
//number of elements in partition cells
n1=2;
n2=2;
n3=3;
//finding number of ordered partitions
p=factorial(n)/(factorial(n1)*factorial(n2)*factorial(n3));
disp('Number of ordered partitions is:',p);
Output:
"Number of ordered partitions is:"
210.
b. Unordered partitions
Aim: Let the set S has 7 elements. Write a scilab code to find the number of unordered partitions of S into 3 cells with 2, 2 and 3 elements.
Scilab Code:
clc;clear;
n=7;//total number of elements in S
//number of elements in partition cells
n1=2;
n2=2;
n3=3;
k1=2;//number of cells have 2 elements
k2=1;//number of cells have 3 elements
//finding number of ordered partitions
op=factorial(n)/(factorial(n1)*factorial(n2)*factorial(n3));
//finding unordered partition
p=op/(factorial(k1)*factorial(k2));
disp('Number of unordered partitions is:',p);
Output:
"Number of unordered partitions is:"
105.
Practical No. 8: Graph Theory
a. Paths and connectivity
Aim: For the graph below, write a scilab code to determine which of the following walks are trails, paths, circuits, or simple circuits.
a. $𝑣_1𝑒_1𝑣_2𝑒_3𝑣_3𝑒_4𝑣_3𝑒_5𝑣_4$ b. $𝑒_1𝑒_3𝑒_5𝑒_5𝑒_6$ c. $𝑣_2𝑣_3𝑣_4𝑣_5𝑣_3𝑣_6𝑣_2$ d. $𝑣_2𝑣_3𝑣_4𝑣_5𝑣_6𝑣_2$ e. $𝑣_1𝑒_1𝑣_2𝑒_1𝑣_2$ f. $𝑣_1$
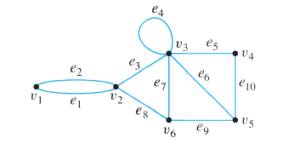Scilab Code:
clc;clear;
A=[0 1 0 0 0 0;1 0 1 0 0 0;0 1 1 1 0 0;0 0 1 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];
disp('Adjacency matrix of A is:',A);
disp('This walk has a repeated vertex but does not have a repeated edge, so it is a trail from v1 to v4 but not a path.');
B=[0 1 0 0 0 0;1 0 0 1 0 0;0 0 0 1 0 0;0 1 1 0 0 0;0 0 1 0 0 0;0 0 0 0 0 0];
disp('Adjacency matrix of B is:',B);
disp('This is just a walk from v1 to v5. It is not a trail because it has a repeated edge.');
C=[0 0 0 0 0 0;0 0 1 0 0 1;0 1 0 1 1 1;0 0 1 0 1 0;0 0 1 1 0 0;0 1 1 0 0 0];
disp('Adjacency matrix of C is:',C);
disp('This walk starts and ends at v2, and does not have a repeated edge, so it is a circuit. Since the vertex v3 is repeated in the middle, it is not a simple circuit.');
D=[0 0 0 0 0 0;0 0 1 0 0 1;0 1 0 1 0 0;0 0 1 0 1 0;0 0 0 1 0 1;0 1 0 0 1 0];
disp('Adjacency matrix of D is:',D);
disp('This walk starts and ends at v2, does not have a repeated edge, and does not have a repeated vertex. Thus it is a simple circuit.');
E=[0 1 0 0 0 0;1 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];
disp('Adjacency matrix of E is:',E);
disp('This is just a closed walk starting and ending at v1. It is not a circuit because edge e1 is repeated.');
F=[0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];
disp('Adjacency matrix of F is:',F);
disp('The first vertex of this walk is the same as its last vertex, but it does not contain an edge, and so it is not a circuit. It is a closed walk from v1 to v1.');
Output:
"Adjacency matrix of A is:"
0. 1. 0. 0. 0. 0.
1. 0. 1. 0. 0. 0.
0. 1. 1. 1. 0. 0.
0. 0. 1. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
"This walk has a repeated vertex but does not have a repeated edge, so it is a trail from v1 to v4 but not a path."
"Adjacency matrix of B is:"
0. 1. 0. 0. 0. 0.
1. 0. 0. 1. 0. 0.
0. 0. 0. 1. 0. 0.
0. 1. 1. 0. 0. 0.
0. 0. 1. 0. 0. 0.
0. 0. 0. 0. 0. 0.
"This is just a walk from v1 to v5. It is not a trail because it has a repeated edge."
"Adjacency matrix of C is:"
0. 0. 0. 0. 0. 0.
0. 0. 1. 0. 0. 1.
0. 1. 0. 1. 1. 1.
0. 0. 1. 0. 1. 0.
0. 0. 1. 1. 0. 0.
0. 1. 1. 0. 0. 0.
"This walk starts and ends at v2, and does not have a repeated edge, so it is a circuit. Since the vertex v3 is repeated in the middle, it is not a simple circuit."
"Adjacency matrix of D is:"
0. 0. 0. 0. 0. 0.
0. 0. 1. 0. 0. 1.
0. 1. 0. 1. 0. 0.
0. 0. 1. 0. 1. 0.
0. 0. 0. 1. 0. 1.
0. 1. 0. 0. 1. 0.
"This walk starts and ends at v2, does not have a repeated edge, and does not have a repeated vertex. Thus it is a simple circuit."
"Adjacency matrix of E is:"
0. 1. 0. 0. 0. 0.
1. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
"This is just a closed walk starting and ending at v1. It is not a circuit because edge e1 is repeated."
"Adjacency matrix of F is:"
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
"The first vertex of this walk is the same as its last vertex, but it does not contain an edge, and so it is not a circuit. It is a closed walk from v1 to v1."
b. Minimum spanning tree
Aim: Write a scilab code to find minimum spanning tree for the following graph by using Kruskal’s algorithm.
