Definition: Set
A well-defined collection of distinct objects is called a set.
e.g. {1,2,3,4,5}, {a,b,c} etc.
Note:
1) Set is always denoted by A, B, C etc.
2) Elements of a set are denoted by a, b, c, x, y, z etc.
3) If ‘a’ is an element of set ‘A’ then we write $a\in\ A$, otherwise, $a\notin A$.
Methods of writing sets
Roster form or list method
In this method we list all the elements of set separated by comma’s and enclosed within braces.
e.g. A={1,2,3,4,5} B={a,b,c}
Rule method or set-builder form
In this method the common characteristic of all the elements is defined.
e.g. $A=\lbrace x|x\in\mathbb{N},x\le5 \rbrace$
$B=\lbrace x|x^2+2x+3=0,x\in\mathbb{R} \rbrace$
Number System
Natural numbers: $\mathbb{N}=\lbrace 1,2,3,…\rbrace$
Whole numbers: $\mathbb{W}=\lbrace 0,1,2,3,…\rbrace$
Integers: $\mathbb{Z}=\lbrace …-3,-2,-1,0,1,2,3,…\rbrace$
Rational numbers: the set of the form $\mathbb{Q}=\lbrace \frac{p}{q}, q\neq0,p,q\in\mathbb{Z}\rbrace$ is called set of Rational Number.
Irrational numbers: The number which is not rational is called irrational.
Real numbers: $\mathbb{R}=\mathbb{Q}\cup\mathbb{Q}^c$
Complex numbers: $\mathbb{C}=\lbrace x+iy|x,y\in\mathbb{R}, i=\sqrt{-1} \rbrace$
Computational Logic and Discrete Structure: Set Theory
Subset
The set A is called subset of B if all the elements of A are also the elements of B. It is denoted by $A\subseteq B$.
e.g. 1) A={1,2,3} B={1,2,3,4,5}
$\therefore A\subseteq B$
2) C={a,b,c} D={b,d}
$\therefore C\subseteq D$
Proper set
The set A is called proper subset of B if all the element of A are also in B and there exists at least one element in B which is not in A.
e.g. A={a,b,c} B={a,b,c,d,e}
$\therefore A\subset B$
Equal sets
The set A and B are equal if all the elements of A are in B and all the element of B are also in A.
e.g. $A=B$ iff $A\subseteq B$ and $B\subseteq A$
Book for Discrete Mathematics : Buy
Null set or Empty set
The set having no elements is called denoted by $\phi$ or
E.g. $A=\lbrace x|2x^2-3=0, x\in\mathbb{Z} \rbrace$
$=\lbrace x|2x^2=3, x\in\mathbb{Z}\rbrace$
$=\lbrace x|x^2=\frac{3}{2}, x\in\mathbb{Z}\rbrace$
$=\lbrace x|x=\pm\sqrt{\frac{3}{2}}, x\in\mathbb{Z}\rbrace=\phi$
Universal Set
In a discussion, all the sets are considered as a subset of a big set called universal set. It is denoted by U.
Note:
1) Every set is subset of Itself. i.e. $A\subseteq A$
2) Empty set is subset of any set. i.e. $\phi \subseteq A$
3) For any set A, $A\subseteq U$.
Computational Logic and Discrete Structure: Set Theory
Power set
A set of all subsets of A is called power set of A and it is denoted by $P(A)$.
e.g. $A=\lbrace 1, 2 \rbrace$
$P(A)=\lbrace \phi, \lbrace 1 \rbrace, \lbrace 2 \rbrace, \lbrace 1, 2 \rbrace \rbrace$
$A=\lbrace 1, 2, 3 \rbrace$
$P(A)=\lbrace \phi, \lbrace 1 \rbrace, \lbrace 2 \rbrace, \lbrace 3 \rbrace , \lbrace 1, 2 \rbrace, \lbrace 2, 3 \rbrace, \lbrace 1, 3 \rbrace, \lbrace 1, 2, 3 \rbrace \rbrace $
Example: Find $P(\phi)$, $P(P(\phi))$
Solution: $P(\phi)=\lbrace \phi, \lbrace \phi \rbrace \rbrace $
$P(P(\phi))=\lbrace \phi, \lbrace \phi \rbrace, \lbrace \lbrace \phi \rbrace \rbrace, \lbrace \phi, \lbrace \phi \rbrace \rbrace \rbrace $
Operations on sets
1) Union: Let A and B be two sets and U be universal set. The union of A and B is the set of all the elements of U which belongs to A or to B or to both and it is denoted by $A\cup B$.
i.e. $A\cup B=\lbrace x\in U|x\in A\ \text{or}\ x\in B\ \text{or}\ x\in \text{Both} \rbrace$
2) Intersection: Let A and B be two sets and U be universal set. The intersection of A and B is the set of all the elements of U which belongs to both A and B and denoted by $A\cap B$.
i.e. $A\cap B=\lbrace x\in U|x\in A\ \text{and} \ x\in B \rbrace$
3) Complement of set: Let A be a set and U be a universal set. The complement of A is the set of all the elements in U which do not belong to A and denoted by $A^c$ or $\bar{A}$.
i.e. $A^c=\lbrace x\in U|x\notin A \rbrace$
4) Difference of two sets: Let A and B be two sets and U be a universal set the difference of two sets A and B (or relative complement of B in A) is a set of all the elements of A which are not in B, and it is denoted by $A-B$ or $A\backslash B$.
i.e. $A\backslash B=\lbrace x\in A|x\notin B \rbrace $
5) Symmetric difference: The symmetrical difference of two sets A and B is denoted and defined an $A\oplus B \ (or\ A\triangle B) =(A\backslash B)\cup(B\backslash A)$.
Computational Logic and Discrete Structure: Set Theory
Example: Let $U=\lbrace 1, 2, 3,…, 10 \rbrace$
$X=\lbrace 1, 2, 3, 4, 5 \rbrace$
$Y=\lbrace y|y=2x, x\in X \rbrace$
$Z=\lbrace z|z^2-9z+14=0 \rbrace$
Find (i) $X\cap Y$ (ii) $Y\cup Z$ (iii) $X-Z$ (iv) $Y^c$ (v) $X^c-Z^c$ (vi) $(X-Z)^c$ (vii) $X\oplus Y$
Solution: $U=\lbrace 1, 2, 3,…, 10 \rbrace$
$X=\lbrace 1, 2, 3, 4, 5 \rbrace$
$Y=\lbrace 2, 4, 6, 8, 10 \rbrace$
$Z=\lbrace z|z^2-9z+14=0 \rbrace$
$=\lbrace z|(z-7)\ (z-2)=0 \rbrace $
$=\lbrace z|z-7\ or\ z-2=0 \rbrace $
$=\lbrace z|z=7\ or\ z=2 \rbrace $
$Z=\lbrace 2, 7 \rbrace $
(i) $X\cap Y=\lbrace 2, 4 \rbrace$
(ii) $Y\cup Z=\lbrace 2, 4, 6, 7, 8, 10 \rbrace $
(iii) $X-Z=\lbrace 1, 3, 4, 5 \rbrace $
(iv) $Y^c=\lbrace 1, 3, 5, 7, 9 \rbrace $
(v) $X^c-Z^c=\lbrace 7 \rbrace $
(vi) $(X-Z)^c=\lbrace 1, 3, 4, 5 \rbrace $
(vii) $X\oplus Y=\lbrace 1, 3, 5, 6, 8, 10 \rbrace $
Algebra of sets
Idempotent Law:
1) $A\cup A=A$
2) $A\cap A=A$
Commutative Law:
1) $A\cup B=B\cup A$
2) $A\cap B=B\cap A$
Associative Law:
1) $(A\cup B)UC=A(B\cup C)$
2) $(A\cap B)\cap C=A\cap(B\cap C)$
Distributive Law:
1) $A\cup(B\cap C)=(A\cup B)\cap(A\cup C)$
2) $A\cap(B\cup C)=(A\cap B)\cup(A\cap C)$
Identity Law:
1) $A\cup\ U=U \ \text{and} \ A\cup \phi=A$
2) $A\cap\ U=A \ \text{and} \ A\cap \phi=\phi$
Involution Law:
$(A^c)^c=A$
Complement Law:
1) $A \cup A^c=U$
2) $A \cap A^c=\phi$
DeMorgan’s Law:
1) $(A\cup B)^c=A^c \cap B^c$
2) $(A\cap B)^c=A^c \cup B^c$
Example: In a college 100 student have access to three software packages, A, B and C. 28 did not use any software, 8 used only package A, 26 used only packages B, 7 used only packages C, 10 used all three packages, 13 used both A and B. Draw a Venn diagram with all sets enumerated as for as possible. Label the two subsets which cannot be enumerated as x and y, in any order. If twice as many students used package B as package A write down a pair of simultaneous equation in x and y. Solve these equations to find x and y how many students used packages C?
Solution:
i) Venn Diagram
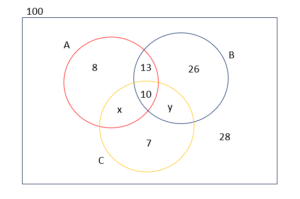
ii) Since, twice as many students used packages B as packages A.
$\therefore 3+10+26+y=2(8+3+10+x)$
$\therefore39+y=2(21+x)$
$\therefore39+y=42+2x$
$\therefore2x-y=-3$
Also, $8+3+10+26+7+28+x+y=100$
$\therefore 82+x+y=100$
$\therefore x+y=18$
iii) $2x-y=-3$
$x+y=18$
$2x-y=-3$
$x+y=18$
————————-
$3x=15$
$\therefore x=\frac{15}{3}$
$\therefore x=5$
$\therefore 5+y=18$
$\therefore y=13$
Now, No. of students using package C
$=x+y+10+7$
$=5+13+10+7$
$=35 $
Example: Given the following universal set U and it’s two subsets P and Q.
Where $U=\lbrace x|x\in \mathbb{Z}, 0\le x\le 10 \rbrace$
$P=\lbrace x|x\ is\ prime\ number \rbrace$
$Q=\lbrace x|x^2<70 \rbrace$
Draw a Venn diagram for the above.
List the element in $P^c \cap Q$.
Solution:
$U=\lbrace x|x\in \mathbb{Z}, 0\le x\le 10 \rbrace$
$=\lbrace 0,1,2,3,4,5,6,7,8,9,10 \rbrace$
$P=\lbrace x|x\ is\ prime\ number \rbrace$
$=\lbrace 2,3,5,7 \rbrace$
$Q=\lbrace x|x^2<70 \rbrace$
$=\lbrace 0,1,2,3,4,5,6,7,8 \rbrace$
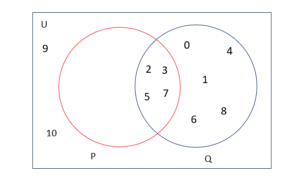
i) Venn Diagram
ii) $P^c=\lbrace 0,1,4,6,8,9,10 \rbrace $
$P^c \cap\ Q=\lbrace 0,1,4,6,8 \rbrace $
Finite and Infinite sets
A set S is said to be finite if it has exactly m elements where m is some non-negative integer and we write n(s)=m or |s|=m.
A set which is not finite is called Infinite.
e.g. $A=\lbrace x|x\in \mathbb{Z}, 0\le x\le 10 \rbrace $
$=\lbrace 0,1,2,…..,10 \rbrace $
$\therefore |A|=10$
$\therefore$ A is finite.
Inclusion-Exclusion Principle
Let A and B be two sets. Then
$n(A \cup B)=n(A)+n(B)-n(A \cap B)$
For three Sets A, B and C
$n(A\cup B \cup C)=n(A)+n(B)+n(C)+n(A \cap B)-n(B \cap C)-n(A \cap C)+n(A \cap B \cap C)$
Computational Logic and Discrete Structure: Set Theory
Duality
Let E be a set equation. The dual $E^*$ of E is obtained by replacing $ U, \phi, \cup, \cap $ in E by $ \phi, U, \cap, \cup $ respectively.
E.g.$(U \cup A)\cap(\phi \cup A)$
The dual is $(\phi\cap A)\cup(U\cap A)$
Example: Suppose a list A contains 30 students in a mathematics class, and a list B contains the 35 students in an English class and suppose there are 20 names on both lists. Find the numbers of students .
i) Only on list A ii) Only on list B iii) on list A or B (or Both) iv) On exactly one list.
Solution:
Let A Denoted students in mathematics. B denoted students in English class.
$\therefore n(A)=30 \ \text{and} \ n(B)=35 \ \text{and} \ n(A \cap B)=20$
i) Only on list A
$=n(A\backslash B)$
$=n(A)-n(A\cap B)$
$=30-20$
$=10$
ii) Only on list B
$=n(B\backslash A)$
$=n(B)-n(A\cap B)$
$=35-20$
$=15$
iii) On list A or B(or both)
$=n(A\cup B)$
$=n(A)+(B)-n(A\cap B)$
$=30+35-20$
$=40$
iv) On exactly one list
$=n(A\backslash B)+n(B\backslash A)$
$=10+15$
$=25$
Partition of a set
A partition of a set A is a collection $\lbrace A_1,A_2,A_3,……A_n \rbrace $ of nonempty subsets of A such that $A_1 \cup A_2 \cup \ldots \cup A_n=A$ and all $A’s$ are mutually disjoint or pairwise disjoint.
e.g. $A_i\cap A_j=\phi, \forall \ i,j=1,2,3, \ldots, n$
Principle of mathematical induction
Step(1): Basic step
i.e. $P(1)$ is true
Step(2):Inductive step
Assume that $P(k)$ is true and prove that $P(k+1)$ is true.
Example: Use mathematical induction to prove that
$1+2+3+\ldots+n=\frac{n(n+1)}{2}, \forall \ n\in \mathbb{N}$.
Solution:
Let $P(n):1+2+3+\ldots+n=\frac{n(n+1)}{2}, \forall \ n\in \mathbb{N}$
Step(1): Basic step
For n=1
L.H.S = 1
R.H.S=$\frac{1(1+1)}{2}=1$
$\therefore$ L.H.S=R.H.S
$\therefore$ P(1) is true.
Step(2): Inductive step
Assume that $P(k)$ is true.
e.g. $1+2+3+\ldots+k=\frac{k(k+1)}{2}$
To prove that $P(k+1)$ is true.
i.e. to prove that
$1+2+3+\ldots+k+(k+1)=\frac{(k+1)(k+2)}{2}$
Consider,
L.H.S.$=1+2+3+\ldots.+k+(k+1)$
$=\frac{k(k+1)}{2} +(k+1) $
$=(k+1)(\frac{k}{2}+1)$
$=(k+1)(\frac{k+2}{2})$
$=\frac{(k+1)(k+2)}{2}$
= R.H.S.
$\therefore$ P(k+1) is true.
Hence, P(n) is true for all $n\in \mathbb{N}$.
Example: Prove by mathematical induction
$\frac{1}{1.2}+\frac{1}{2.3}+\ldots+\frac{1}{n(n+1)} =\frac{n}{n+1}, \forall \ n\in \mathbb{N}$
Solution:
Let $P(n): \frac{1}{1.2}+\frac{1}{2.3}+\ldots+\frac{1}{n(n+1)} =\frac{n}{n+1}, \forall \ n\in \mathbb{N}$
Step(1): Basic step
For n=1
L.H.S. $=\frac{1}{1.2}=\frac{1}{2}$
R.H.S. $=\frac{1}{(1+1)}=\frac{1}{2}$
L.H.S. = R.H.S.
Step(2): Inductive step
Assume that P(k) is true.
i.e. $\frac{1}{1.2}+\frac{1}{2.3}+\ldots+\frac{1}{k(k+1)} =\frac{k}{k+1}$
To prove P(k+1) is true
i.e. to prove that
$\frac{1}{1.2}+\frac{1}{2.3}+\ldots+\frac{1}{k(k+1)}+\frac{1}{(k+1)(k+2)}=\frac{k+1}{k+2}$
Consider
L.H.S $=\frac{1}{1.2}+\frac{1}{2.3}+\ldots+\frac{1}{k(k+1)}+\frac{1}{(k+1)(k+2)}$
$=\frac{k}{k+1}+\frac{1}{(k+1)(k+2)}$
$=\frac{1}{(k+1)}\left[k+\frac{1}{k+2}\right]$
$=\frac{1}{(k+1)}\left[\frac{k^2+2k+1}{k+2}\right]$
$=\frac{1}{(k+1)}\left[\frac{(k+1)^2}{k+2}\right]$
$=\frac{K+1}{K+2}$
=R.H.S
$\therefore$ P(k+1) is true.
Computational Logic and Discrete Structure: Set Theory
Example: Use Mathematical induction to prove that $n^3-n$ is divisible by 3 whenever n is positive integer.
Solution: Let $P(n): n^3-n$ is divisible by 3.
i.e. $P(n):n^3-n=3k, \ \text{for some} \ k \in \mathbb{Z}$
Step(1): Basic step
For n=1
$n^3-n=1^3-1=0=3(0)$ which is divisible by 3.
$\therefore$ P(1) is true.
Step(2): Inductive step
Assume that P(K) is true
i.e. $k^3-k=3m \ \text{for some} \ m \in \mathbb{Z}$
To prove that P(k+1) is true
i.e. to prove that,
$(k+1)^3-(k+1)=3m \ \text{for some} \ m \in \mathbb{Z}$
Consider,
L.H.S $=(k+1)^3-(k+1)$
$=k^3+3k^2+3k+1-k-1$
$=(k^3-k)+3(k^2+k)$
$=3m+3(k^2+k)=3(m+k^2+k)$
$=3p$, where $p=m+k^2+k \in \mathbb{Z}$
$\therefore (k+1)^3-(k+1)$ is divisible by 3.
i.e. P(k+1) is true.
$\therefore$ P(n) is true $\forall \ n \in \mathbb{N}$.
Example: Use mathematical induction to prove that for all integer $n\geq 3, 2n+1<2^n$
Solution:
Let $P(n): 2n+1<2^n, n\geq 3$.
Step(1): Basic step
For $n=3$
L.H.S $=2(3)+1=7$
R.H.S $=2^3=8$
$\therefore$ L.H.S<R.H.S
P(1) is true.
Step (2): Inductive step
Assume that P(k) is true
i.e. $2k+1<2^k$
Now to prove that P(k+1) is true.
i.e. to prove that $2(k+1)+1<2^{k+1}$
L.H.S. $=2(k+1)+1$
$=2k+2+1$
$=(2k+1)+2$
$<2^k+2$
$<2^k+2^k$
$=2.2^k$
$=2^{k+1}$
L.H.S < R.H.S